�@�@�@�@
���W�I�w�K�̂��߂̍��Z�����~�j�����|�C���g
�T�D�^���ʂ̕ۑ��E�͂˂�����W���E�G�l���M�[
�X�D�d�C�͐��̗����C���[�W�P�O�D�R���f���T�[�ɒ~����ꂽ�Ód�G�l���M�[�̓R���f���T�[�̂ǂ��ɑ��݂���̂�
�P�P�D�u�L���q�z�b�t�̖@���v�̎w���ɂ���
�P�Q�D�t���~���O�̍���̖@���ƉE��̖@��
�@
�P�D���_�������K�����(���)
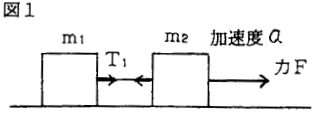
�}�P�̑��u�ŁC�����xa�ƒ����s�P�����߂�B
�@�@�@�@
�@�@�@���̉�
�@�@�@![]()
�@�@�@![]()
�@�@�@�ł���B�}�Q�̂悤�ȏꍇ�C�����s�P�C�s�Q�y�������xa�͂ǂ��Ȃ邩�B�v�Z�������ɓ�����B
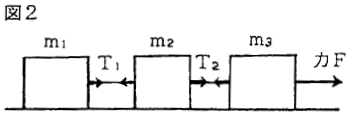
(��) m�Q�Cm�R�������܂Ƃ߂Đ�̖���m�Q�ƍl����C
�@![]() �@���@
�@���@![]()
�@![]() �@���@
�@���@![]() �@
�@
�@ �@����ɁCm�P�Cm�Q�����ɂ��čl����ƁC
�@![]() �@���@
�@���@![]() �@
�@
�@�@�R���A�������������������́C���w�Ƃ��Ă͐��������C�����̔��z�Ƃ��Ă͕n���ł���B
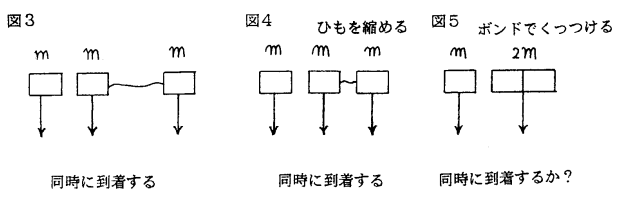
(���) ���̂̎��R�����̗l�q�͎��ʂɂ��Ȃ����Ƃ��C���̐}�����Ƃɐ�������B
(��)
�Ђ��̒���������ɒZ�����Ă������Ɍ����l����B��������ƁC���̂ǂ�����������������Ƃ����ċ}�ɗ����̗l�q���ς��Ƃ����͕̂s���R�ł���B���������Ď��ʂ��Q�{�ɂȂ��Ă����������̎d���i�����ɒn�ʂɒ����j������ƍl���Ȃ���Ȃ�Ȃ��B�i�K�����C�̎v�l������蒼�ϓI�ł͂Ȃ����낤���B�j
(���)
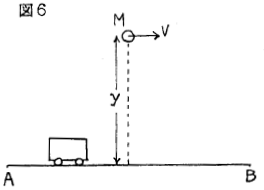
�����`�a�Ԃ��W�b�����铙���^�����Ă���Ԃ�����B���̎Ԃ��`�a�Ԃ�1/4�̋����𑖂�����C�`�a�Ԃ̒�����̍���y[m]�ɂ���{�[���l���������˂����B���̃{�[���l���a�n�_�ŎԂɏՓ˂���Ƃ��C�{�[���̍���y�Ɛ��������ɓ����o����鑬�xv�͂����炩�B�d�͉����x��g[m/s�Q]�Ƃ��C�`�a�Ԃ�x [m]�Ƃ���B
(��)![]()
![]()
�@�����I��@�͂����邤�܂����@�ł��邪�C�Ջ@���ςɑΉ����Ȃ���Ȃ炸�C���ł�������Ƃ͂�����Ȃ��B�����I��@����ł��邪�C�������w�I�v�Z�ʂ������Ȃ��Ă�����ʓI�ȉ�͓I��@�����k�ɑ̌����������B
�}�V�̂悤�ɁC�����ʂƊp�x�������X�����Ζʏ�ŁC�Ζʂɑ����̊p�x�C�����xv���Ń{�[���𓊂��グ���Ƃ��̎Ζʏ�̓��B�����k�����߂�B
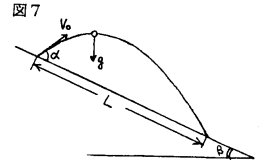
(�����I��@)
�@�}�W�̂悤�ɁC���̐}���p�x��������]�����āC�Ζʂ������ɂȂ�悤�ɂ���ƁC�{�[���̐��������̉����x��g sin���C���������̉����x��g cos���̉^���ɒu�������邱�Ƃ��ł���B���Ƃ́C���������������x�^���ł��邱�Ƃɒ��ӂ���C�ǂ̋��ȏ��ɂ�����Ε����˂̗��Ɠ��l�ɉ����āC���̖��̏ꍇ�͂�����̉�@�̂ق����v�Z���e�Ղł���B
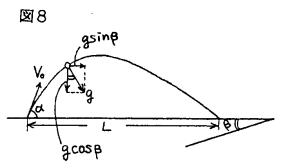
(��͓I��@)
�@�}�X�̂悤��x�Cy���W�����Ƃ�ƁC�{�[���̔�Ղ�y��ax�Q�{bx�i�W��a�Cb��v���C���C���ŕ\����j�C�Ζʂ�y��cx�ic���|tan���j�ŕ\����B���̌�_�o��x���Wx�������߂���C�k���k��x���^cos���ŋ��߂邱�Ƃ��ł���B���̖��̏ꍇ�C��͓I���@�͌v�Z�͂�������ł��邪�C�Ζʂ������łȂ��ꍇ�ɂ��Ή��ł��C����ʓI�ł���B
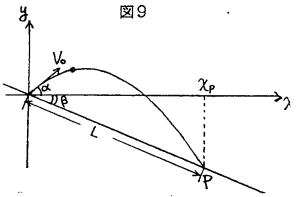
(���)
�Î~���Ă��鎿���l�̕��̂ɁC����v���C����m�̕��̂��Փ˂���B�̂̂͂˂�����W����e�Ƃ��鎞�C�Փˌ�̓�̕��̂̑��x�����߂�B�i�Փ˂͈꒼����ł�������̂Ƃ���B�j
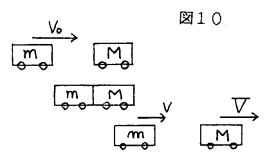
�@���̖����������Ȃ��ŃT�b�Ɖ�����悤�ɂȂ��ė~�����̂����C�Ȃ��Ȃ����߂͂��܂������Ȃ��B�Q�N�ŕ����𗚏C����ꍇ�ȂǁC
�@(1) �^���ʂ̎��͗����C�͂˂�����W���̎������Ȃ��B
�@(2) ��̎��͂ł������C����������v�Z�͂��Ȃ��B
�@(3) ���������C�v�Z�ԈႢ�ɋC�t���Ȃ��B
�ȂǁC���낢��ȃn�[�h��������B�t�Ɍ����C������������ƂŁC���̗��ĕ��C�v�Z�́C�v�Z�ԈႢ�̃`�F�b�N�����o���ł����ł���B���ɁC���������������ƂɁCe��1.0�ł͂ǂ��Ȃ邩�C�l��m�ł͂ǂ��Ȃ邩�C���ۂ̉^�������͂ǂ��Ȃ邩��,�l���Ȃ���v�Z�ԈႢ�̃`�F�b�N�����邱�Ƃ́C�����I�ȍl��������Ă��ő�ϗL���ł���Ǝv���B�����C��x����Ă��S�̂�������Ɨ�������̂͑�ςł���B���Ԃ������ĉ��x�����K�v������B�܂��C�Փ˂ɂ���Ď�����G�l���M�[���v�Z������̂��d�v�ł���B����͂܂��Ce���P���ǂ����ŃG�l���M�[���ۑ�����邩�ǂ����������Ōv�Z���Ă݂邢���@��ƂȂ�B
(1) ���Α��x
�@���Α��x�̎��u�a�`���u�`�|�u�a�C�u�Q�P���u�P�|�u�Q�ɂ����āC�Y���ɂ��ẮC�u�a�`���u�Q�P��(�u�a)�`�C(�u�Q)�P�ƍl���C�`�̑��x�C�P�̑��x�ɏd�_�����邱�Ƃɒ��ڂ���B����́C���Ƃ��]�E�K���Ƃ����̂͋T�̂��ƂŁC�N�}�l�Y�~�Ƃ����̂͑l�̂��Ƃ��w���Ă���̂Ɠ����ɍl����B���Α��x�̎� �u�a�`���u�`�|�u�a�C�u�Q�P���u�P�|�u�Q�ɂ����āC�u�`�|�u�a���u�P�|�u�Q�́C�u�`���u�P����̂ŁC�|�u�a��|�u�Q�ŏC�����Ă���B�܂�C�a��Q�������ƍl���C�`��P���u����v�ƍl����ƁC�����������Ă���Ƃ��ɂ́u����̑��x�v���玩���̑��x�����������̂��������猩���u����̑��x�v�ɂȂ�ƍl����B
(2) �����~�^���̎����̎�
�@�s���Q��r�^v���Q�^�� �� v�s���Q��r�C���s���Q�ƒ����Ă݂�ƁC
�@�@�@�@�@�@�@�@�����~�P��]�̎��ԁ��P��]�̋���
�@�@�@��]�̑����~�P��]�̎��ԁ��P��]�̊p�x
�ƍl������B�����̌����́C������Ƃ����펯�i�m���j�łł��オ���Ă���B�������C�����I�Ӗ���v���Q��r�^�s�C�ց��Q�^�s�ł͂���B
(3) �R���f���T�[�̐ڑ�
�@�d�C�e���b�͓d�ׂ̂��܂�Ղ���\���B���������āC�P�^�b�͓d�ׂ̂��܂�ɂ�����\���B����ڑ��ł́C���ꂼ��̂��܂�Ղ��̘a���S�̂̂��܂�Ղ��ɂȂ邩��C�b���b�P�{�b�Q�ł���B����ڑ��ł́C���ꂼ��̂��܂�ɂ����̘a���S�̂̂��܂�ɂ����ł��邩��C�P�^�b���P�^�b�P�{�P�^�b�Q�ł���B
(4) �I�[���̖@��
�@��R�i���W�X�^���X�j�q�͓d���̗���ɂ�����\������C����Ղ��͂P�^�q�Ŏ������B���������āC
�@�@![]()
�i�P�ʓd��������̓d���̋����j�ƍl������B
(5) ��R�̐ڑ�
�@�q�͗���ɂ����C�P�^�q�͗���Ղ��ƍl����ƁC����ڑ��ł́C���ꂼ��̗���ɂ����̘a���S�̗̂���ɂ����ł��邩��C�q���q�P�{�q�Q�ł���B����ڑ��ł́C����Ղ��̘a���S�̗̂���Ղ�������C�P�^�q���P�^�q�P�{�P�^�q�Q�ł���B
�@���q�̉^������C�̂̈��͂����@�́C�������ア��������B�m�̕��q������Ƃ��āC���Ƃ��C
(1)�����̂ɕ��q�������Ă��āC�m�^�R���C���ꂼ��x�Cy�Cz�����ɓ�������v�ʼn^�����Ă���Ƃ�����́B
(2)�����̂ɓ����Ă��āC���낢��ȉ^�������Ă���Ƃ�����́B
(3)���`�̗e��ɓ����Ă��āC���낢��ȉ^�������Ă���Ƃ�����́B
�Ȃǂ��L���ł���B�������S�Ă̏ꍇ�œ�������
�@�@�@�@![]() �im�F���q�̎��ʁC�m�F���q���C�u�F�̐ρj
�im�F���q�̎��ʁC�m�F���q���C�u�F�̐ρj
��^����̂ł��邪�C�ؓ��̒����c�_�Ő��k�ɂ͓�������ł���B���ʂ�������ƁC�ꌩ�c�_�̉ߒ���Y��Ă��܂������ł��邪�C���o�������Ǝ��̂悤�ɑ�܂��ɋؓ����v���o������悤�ɂ��Ă���B
�@����k�̗����̂ł��u���k�R�ƂȂ�C���̂悤�ɕ����ł���B
�@�@�@�@
���ς̘b��Cx�Cy�Cz�R�����̘b���G�ł��邪�C���̓��o�ߒ����v���o���ɂ́C����Ȃ�̌��ʂ����邾�낤�B
�@���̏��������Ƃ��C�]���͈ȉ��̂Q�ʂ�̕��@�ŋ����Ă����B
(1)���ʑ��ŐU������Q�̏��������ʂ��������Ƃ��ɂł���g�ʂ�}�ɏ����ē������@
(2)�Q�_����o��g���������ē������@
�Ƃ��낪�C(1)�͂��܂�Ɍo���I�Ō��_�ɋ^�₪�c�邵�C(2)�͂��܂�ɐ��w�I�ʼn��߂�����Ƃ�����_���������B���̕ӂ̎����l���Ď��̂悤�ȓW�J�����݂Ă���B
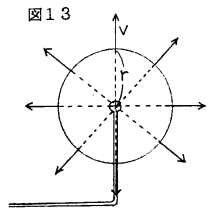
�@�Q�̏����o�C�p�𐅖ʂɐڐG�����ē��ʑ��ŏ㉺�ɐU���������Ƃ��̐��ʂ̗l�q���v�����g��z���č�}�����T�������܂���B���ɓ_�o����k�P�C�_�p����k�Q���ꂽ�_�q�Ŕg�����߂�������߂��������l����B����Ƃ��_�o�C�p����g�̎R�������ɏo���Ƃ���ƁC�_�o���炫���R���_�q�ɓ��������Ƃ��C�_�p���炫���R�͓_�q�������ē_�q�f�܂Ői��ł���B�o�q���p�q�f���k�P�ł���B���̂Ƃ��_�q�Ŕg�����߂��������́C�_�p���炫���g���_�q�ŎR�ɂȂ��Ă��邱�Ƃł���C�_�q�Ŕg����߂��������͓_�p���炫���g���_�q�ŒJ�ɂȂ��Ă��邱�Ƃł���B���̏�����}�Q�����čl����ƁC�_�q�f���R�ł��邱�Ƃ���C�_�p���炫���R���_�q�ŎR�ł��邽�߂ɂ͂q�q�f���i�k�P�|�k�Q�j���g���̐����{�łȂ���Ȃ炸�C�_�q�ŒJ�ł��邽�߂ɂ͂q�q�f���i�k�P�|�k�Q�j���g���̐����{�{���g���łȂ���Ȃ�Ȃ����Ƃ��킩���B
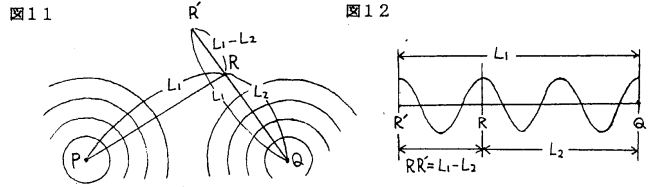
�@�d�C�͐��͎��̂悤�ȗ����̃C���[�W�ɒu����������B
�@�ǂ̕����ɂ������o���X�v�����N���[�̂悤�Ȃ��̂��l����B���C�P�ʎ��Ԃ����莿���p�̗��̂���Ԃ̂���_����ǂ̕����ɂ��ϓ��ɂ킫�o�Ă���ƍl����B���̖̂��x���ρC�킫�o���_���狗��r�̓_�ł̗��̂̑��x��v�Ƃ���ƁC
�@�@�p���ρ~���ar�̋��̕\�ʐρ~v
�@�@�@���ρ~�S��r�Q�~v
����āC
�@�@![]()
�@����C�d���p�̓_�d�ׂɂ�鋗��r�̓_�ł̓d�E�̋����d�́C�N�[�����̖@�����C
�@�@![]() �@�@
�@�@
����́C�d��v�ƒu��������C��̗��̂̂킫�o���̎��Ɠ����ł���B���Ȃ킿�C�d�C�͐��͗��̗̂����̃C���[�W�Œu����������B�ڂɌ����Ȃ���Ԃ̓d�E���C���[�W����Ƃ��C�����̃C���[�W�i���d�C�͐��j�͑�ϗL���ł���C���ۓI�ȏ��\�������̎������̂悤�ȕ����I�C���[�W�ɂȂ���ƁC���g�߂Ȃ��̂ɂȂ�̂ł͂Ȃ����낤���B���̘b�́C���ۂɃt�@���f�[���d�E�⎥�E��\���̂ɕ����I�����C���[�W�œd�C�͐��⎥�͐������C�}�N�X�E�F�����͊w�I�ɂ����̗l�q����͂��悤�Ƃ������Ƃ�C�K�E�X�̒藝�̘b�ɂȂ��Ă��ʔ����B
�@
�P�O�D�R���f���T�[�ɒ~����ꂽ�Ód�G�l���M�[�̓R���f���T�[�̂ǂ��ɑ��݂���̂�����͎��̂悤�ɐ����ł���B
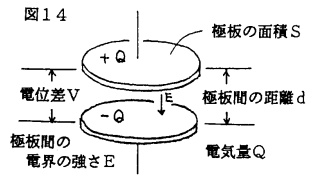
�@�}�̂悤�ɏ[�d����Ă���Ƃ��C�~����ꂽ�Ód�G�l���M�[��
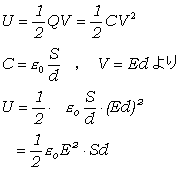 �@
�@
����āC�G�l���M�[�͋ɔԂ̑̐��rd�ɔ�Ⴕ�C���x�����d�Q�^�Q�ŁC���̋�Ԃ��Ȃ킿�d�E�ɒ~�����Ă���B
�@�R���f���T�[�ɂ��Ĉ�ʂ����������C���炽�߂Đ��k�ɖ₢������ƁC���̓����͓d�ׂł�������C�ɔł�������̂��Ƃ������B���ȏ��ł����܂蒍�ӂ���Ă��Ȃ����̂�����̂ŁC���Ў蓖���Ă��������Ƃ���ł���B
�@���l�̎��̓R�C���ɒ~������d���G�l���M�[�ɂ��Ă�������B
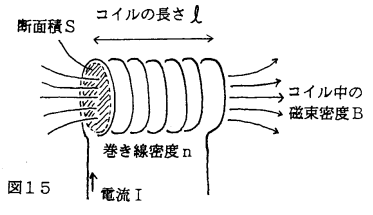
�d���h������Ă��鎩�ȃC���_�N�^���X�k�̃R�C���ɒ~������G�l���M�[��
![]() ----- �@
----- �@
����C
![]() ----- �A
----- �A
�R�C���ɐ����鎩�ȗU���N�d���u��
�@�@![]()
����āC���ȃC���_�N�^���X�k��
![]() -----
�B
-----
�B
�@�C�A�C�B���
�@�@![]()
�R�C���̏ꍇ���C�R���f���T�[�̏ꍇ�Ɠ��l�ɃG�l���M�[�̓R�C�����̑̐��rl�ɔ�Ⴕ�C���x�����g�Q�^�Q�Ŏ��E�ɒ~�����Ă���B
�@�������Ă݂�ƁC�d�E�⎥�E�̂悤�ȁu��v�͋�Ԃ̗l�q��������邽�߂ɕX�I�ɍl����ꂽ���̂ł͂Ȃ��C��̓I�ɃG�l���M�[��~����ƌ����悤�Ȏ��Ԃ������̂ł��邱�Ƃ������͗��������̂ł͂Ȃ����낤���B
(1) �e���ȏ��̈���
�@�`�o�Ŏ�
�@�h�D��H���̌�_�ɗ��ꍞ�ޓd���̑㐔�a�͂O�ł���B
�@II�D��H���̔C�ӂ̂ЂƂ܂��̉�H�ɂ��āC�N�d�͂̑㐔�a�͓d���~���̑㐔�a�ɓ������B
�a�o�Ŏ�
�@�o�ɗ��ꍞ�ޓd���̘a�́C�o���痬��o���d���̘a�ɓ������B�i��P�@���j
�@�N�d�̘͂a�͓d���~���̘a�ɓ������B�i��Q�@���j
�b�o�Ŏ�
�@(1)�d���̕ۑ��@�@����_�ł̓d���̑��a�͂O�ł���B
(2)��H�̋N�d�͂Ɠd���~���@�@��H�̒��̋N�d�̘͂a�͊e��R�ł̓d���~���̘a�ɓ������B
(2) ���ȏ��̈����ł̍���_
�.��P�@���́C����d�����{�C�o��d�����|�Ƃ��đ��a���O�Ƃ��Ă��C����ʁ��o��ʂƂ��Ă��C������傫�Ȗ��_�͂Ȃ��B
�.��Q�@���ł́C�ǂ̋��ȏ����N�d�͂Ɠd���~�����čl���C���҂��������Ƃ���̂́C��P�@���ƌ`�����Ⴂ���ꐫ�Ɍ�����B
�.��Q�@���ŁC�N�d�͉͂��肵���d���̌����ɗ������Ƃ���̂��{�Ƃ��Ă���̂͗ǂ����C�d���~���͉�����̂��{�Ƃ���͍̂�������B
(3) �w����
�.�Ód�C�̕����Łu�d�ʁv�̍l������������w������B�܂��C�I�[���̖@�����u�d���͓d�ʂ̍���������Ⴂ���ɗ���C��R�ɂ��d�ʂ͓d���̌������q�h[��]�~������i�u���q�h�j�v���Ƃ����܂���B
�.�d�r�̋N�d�́E������R�̍��ŁC�N�d�͂́{���̓d�ʂ��������Ƃ����܂���B
�.�L���q�z�b�t�̖@���͎��̌`�Ŏw������B
�@�h�D��H���̔C�ӂ̓_�ŁC���̓_�ɓ���d�����{�C�o��d�����|�Ƃ����㐔�a�͂O�ł���B
�@II�D��H���̔C�ӂ̂ЂƂ܂��̉�H�ɂ��āC�d�ʂ��オ��Ƃ��{�C������Ƃ��|�Ƃ����N�d�́E��R�ɂ��d�ʕω��̑��a�͂O�ł���B
<���_>
�.�u�㐔�a���O�v�Ƃ��铝�ꂵ���`���ŕ\����B
�.��Q�@�����C�d�ʕω����ЂƂ܂�肵�Č��ɖ߂�ƂO�ɂȂ邱�Ƃ͗e�Ղɗ����ł���B
�.��x�������Ă��܂��C��艉�K�ł͋@�B�I�Ƀ~�X�Ȃ��Ή��ł���B�N�d�͂ƒ�R�ɂ��d���~��������ȒP�ł���B
<����_>
���ȏ���Q�l���ނɂ�����鐶�k�͍�������B���ɗ���͂̂悢���k�ɂ݂���B
�Ή��Ƃ��āC���̕ό`�ŗ��҂������ł��邱�Ƃ�����Č����Ă���B
�@�@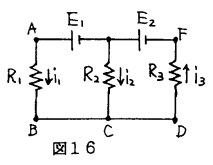
�@�f�_�@�@�@�@�@�@�@�@�@���P�{���Q�����R
�@�`�a�b�c�e�f�`��H�@�@�d�P�{�d�Q���q�P���P�{�q�R���R
����
�@�f�_�@�@�@�@�@�@�@�@�@�|���P�|���Q�{���R���O
�@�`�a�b�c�e�f�`��H�@�@�|�q�P���P�|�q�R���R�{�d�Q�{�d�P���O
�@�d�������E�����͂̌����̓t���~���O�̍���̖@���ŁC���������͐����Ƃ��ɐ�����U���N�d�͂̌����̓t���~���O�̉E��̖@���ŋ��߂���Ƃ����̂͂ǂ̋��ȏ��ɂ���ʓI�ɍڂ��Ă��邱�Ƃł���B���������ۂɐ��k�Ɏ������Ŏ������u��O�ɂ��Ă��̕��������߂�������C�������������肷��ƁC�ȊO�ɖ����Ă���ꍇ���ڂɂ��B�����̈�́C�E����g���̂�������g���̂��Y��Ă��܂����Ƃł��邪�C����ɑ��ẮC�u�����͉̂E�肾����C���������͐�������Ƃ��ɐ�����U���N�d�͂̌����̓t���~���O�̉E��̖@���ŋ��߂�B�v�Ƃ����������I�ȈËL�@������B���ɍ���C�E��͂킩���Ă��C�e�w�C�l�����w�C���w�����ꂼ�ꉽ��\���̂��������Ŗ�������C���u����̐}�Ɋe�w�̌��������킹�邽�߂ɑ̂��Ђ˂��Ă��鐶�k���o����ŁC�Ȃ��Ȃ����m�ȋ�J�������悤�ł���B���̕����Ɋւ��Ă̓A���y�[���̉E�l�W�̖@���ƁC���͐����S���R�ɂ��Ƃ��邱�Ƃɂ��C���̂悤�ɐ������Ă���B
�@�A���y�[���̉E�l�W�̖@���́C�P�V�}�̂悤�ɁC�d�����E��ň������Ƃ��C�e�w���d���C���̎w�����E�̌�����\�����ƂŎ������B������܂����k�ɂ�������������Ă����B
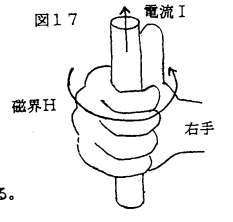
�@�d���h�����E�g�����͂e�͎��̐}�̂悤�ɍl����B
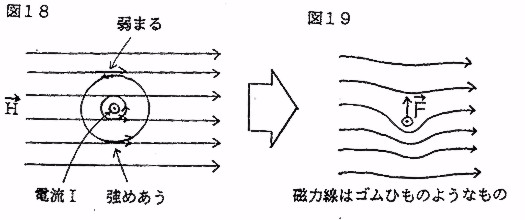
�@���[�����c�͂ɂ��Ă��C�דd���q�̗��ꂪ�d�����ƍl����C���l�ɗ͂̕��������߂���B
�@���E�����^�����铱���ɐ�����U���N�d�͂ɂ��ẮC���[�����c�͂ɂ���ĉ��}�̂悤�ɍl���邱�Ƃɂ���B
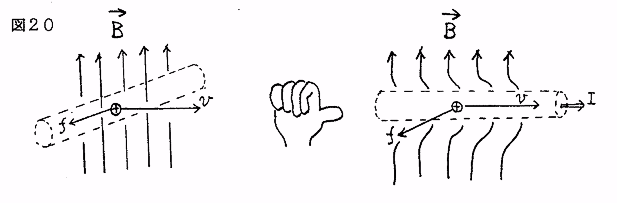
�@�ȏ�̕��@�̓t���~���O�̍���C�E��̖@���������o�������C���V���v���ł���C�����I�ł���Ǝv����B
�@���̊e�搶�����玑������Ă��������܂����B��ϊ��ӂ������܂��B
�@�@�@�@�〈�q���C���@�́C�s���@�_�C�n�Ӂ@���y�C�|�c���V�C�O�c��x�m�v
�@�����W�쐬�ɂ������āC������ŏ���ɕ\���������C���͂�ύX������C�܂��C���Ă������������e�̈ꕔ�����ڂ����Ȃ��������̂�����C���̂��߂Ɋe�҂̈Ӑ}���\���`���Ȃ����̂������������Ƃ���C����͂��ׂĎ��̐ӔC�ł���C����ђv���܂��B
�@�܂��C����Șb���������C�Ƃ����̂��������玑������������B
(�]�쒼�l)